반응형
트리(Tree)
- 노드들이 나무 가지처럼 연결된 비선형 계층적 자료구조
- 계층적인 자료를 표현하는데 이용
- 노드(node)들과 노드들을 연결하는 간선(edge)들로 구성
- 하나의 루트노드를 가짐
트리와 관련된 용어

노드(node)
- 트리를 구성하고 있는 기본요소
- 노드에는 키 또는 값과 하위 노드에 대한 포인터를 가지고 있음
간선(edge)
- 노드와 노드 간의 연결선 (link, branch라고도 부름)
루트 노드(root node)
- 부모가 없는 최상위 노드, 트리는 하나의 루트 노드만을 가짐 (A)
부모 노드(parent node)
- 자신 노드를 가진 노드 (H, I의 부모 노드는 D)
자식 노드(child node)
- 부모 노드의 하위 노드 (노드 D의 자식 노드는 H, I)
형제 노드(sibling node)
- 같은 부모를 가지는 노드 (H, I는 같은 부모를 가지는 형재 노드)
외부 노드(external node, outer node), 단말 노드 (terminal node), 리프 노드(leaf node)
- 자식이 없는 노드 (H, I, J, F, G)
내부 노드 (internal node, inner node), 비 단말 노드 (non-terminal node), 가지 노드 (branch node)
- 단말 노드가 아닌 노드, 자식 노드를 하나 이상 가진 노드 (A, B, C, D, E)
크기(size)
- 자신을 포함한 모든 자식 노드의 개수
- B의 크기: 6
깊이(depth)
- 루트에서 어떤 노드에 도달하기 위해 거쳐야 하는 간선의 수
- 루트 노드의 깊이: 0, D의 깊이: 2
높이(height)
- 어떤 노드에서 리프 노드까지 가장 긴 경로의 간선(Edge) 수
- 리프 노드의 높이 : 0, A 노드의 높이 : 3
레벨(level)
- 루트에서 어떤 노드까지의 간선(Edge) 수
차수(degree)
- 노드의 자식 수
- Leaf node의 degree : 0; A의 degree : 2
경로(path)
- 한 노드에서 다른 한 노드에 이르는 길 사이에 놓여있는 노드들의 순서
- A & H 경로 : A-B-D-H
path length
- 해당 경로에 있는 총노드의 수
- A & H 경로 길이 : 4
width
- 레벨에 있는 노드 수
- Level 2 width : 4
breadth
- 리프 노드의 수
- Breadth : 5
distance
- 두 노드 사이의 최단 경로에 있는 간선(Edge)의 수
- D와 J의 Distance : 3
order
- 부모 노드가 가질 수 있는 최대 자식의 수
- Order 3 : 부모 노드는 최대 3명의 자식을 가질 수 있다.
서브 트리(sub tree)
- 트리 내의 하위 집합 (부분 집합)
- D, H, I 가 하나의 서브 트리
트리의 특징
- 그래프의 한 종류이며 ‘최소 연결 트리’라고도 불림
- 트리는 DAG(Directed Acyclic Graphs, 방향성이 있는 비순환 그래프)의 한 종류
- 단순 순환(Loop)을 갖지 않고, 연결된 무방향 그래프 구조
- 데이터를 순차적으로 저장하지 않기 때문에 비선형 자료구조
- 노드가 N개인 트리는 항상 N-1개의 간선(edge)을 가짐
- 노드 간에 부모 자식 관계를 갖고 있는 계층형 자료구조이며 모든 자식 노드는 하나의 부모 노드만 가짐
- 부모-자식 관계이므로 흐름은 top-bottom 아니면 bottom-top으로 이루어짐
- 순회는 Pre-order, In-order 아니면 Post-order로 이루어짐
- 전위 순회(Pre-order traverse): 루트 -> 왼쪽 자식 노드 -> 오른쪽 자식 노드 순서로 방문하는 순회 방법
- 중위 순회(In-order traverse): 왼쪽 자식 노드 -> 루트 -> 오른쪽 자식 노드 순서로 방문하는 순회 방법
- 후위 순회(Pre-order traverse): 왼쪽 자식 노드 -> 오른쪽 자식 노드 -> 루트 순서로 방문하는 순회 방법
트리의 종류
이진 트리 (Binary Tree)
- 모든 노드가 자식의 노드 수가 2개 이하인 트리
- 정이진 트리(full binary tree): 자식 노드가 0 또는 두 개인 이진 트리
- 완전 이진 트리(complete binary tree): 왼쪽에서부터 채워져 있는 이진 트리, 마지막 레벨을 제외한 모든 레벨이 완전히 채워짐, 마지막 레벨의 경우 왼쪽부터 채워짐
- 변질 이진 트리(degenerate binary tree): 자식 노드가 하나밖에 없는 이진 트리
- 포화 이진 트리(perfect binary tree): 모든 노드가 꽉 차있는 이진 트리
- 균형 이진 트리(balanced binary tree): 왼쪽과 오른쪽 노드의 높이 차이가 1 이하인 이진트리

이진 탐색 트리 (Binary Search Tree, BST)
- 순서화된 이진 트리
- 노드의 왼쪽 자식은 부모의 값보다 작은 값을 가져야 하며 노드의 오른쪽 자식은 부모의 값보다 큰 값을 가져야 함
- 검색을 하기에 용이
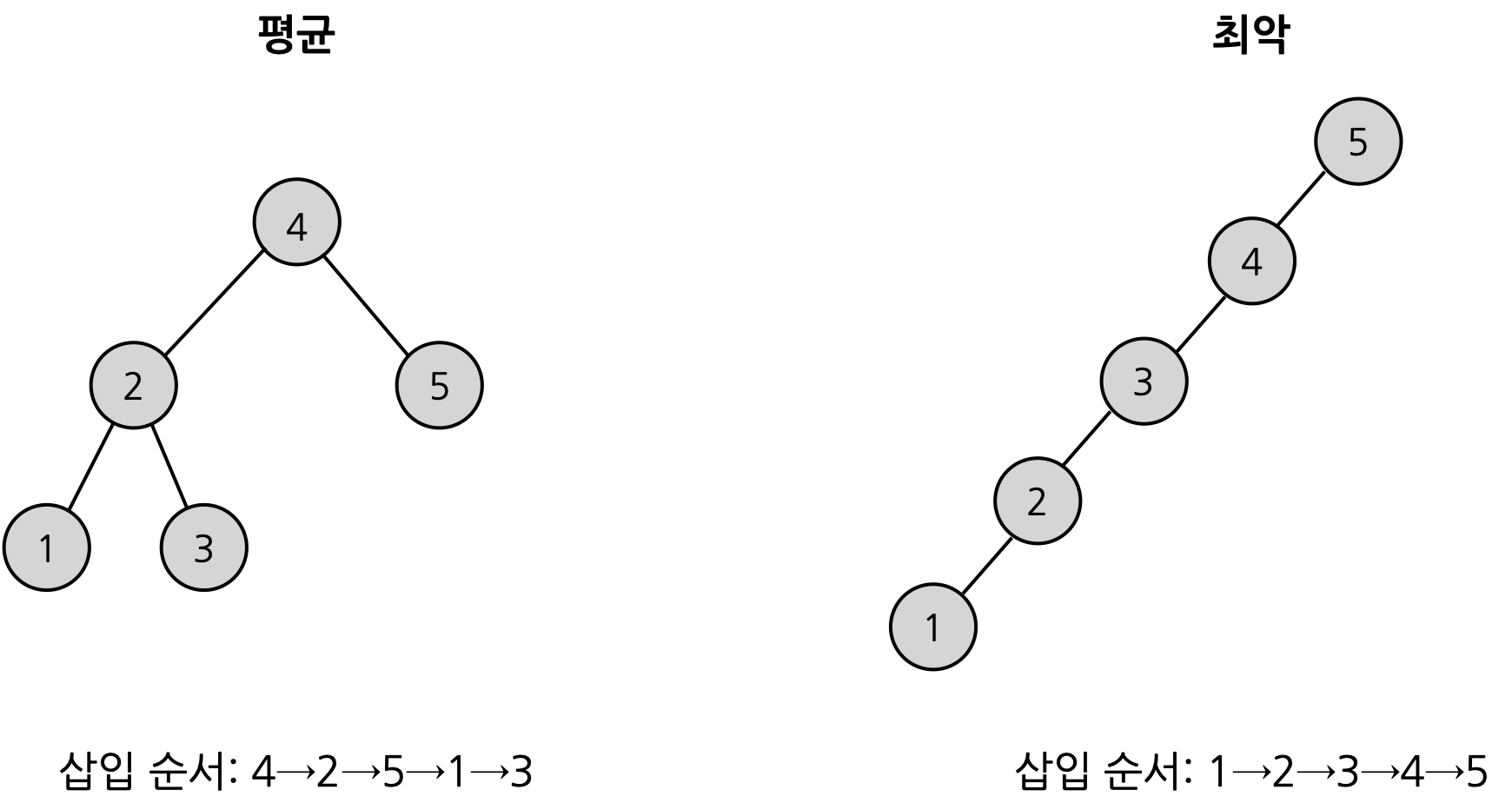
- 보통 요소를 찾을 때 O(logn), 최악의 경우 O(n)
- 삽입 순서에 따라 선형적일 수 있음
AVL 트리 (Adelson-Velsky and Landis Tree)
- 이진 탐색 트리의 최악의 경우 선형적인 트리가 되는 것을 방지하고 스스로 균형을 잡는 이진 탐색 트리
- 두 자식 서브트리의 높이는 항상 최대 1만큼 차이가 남
- 탐색, 삽입, 삭제 모두 시간복잡도가 O(logn)
- 삽입, 삭제를 할 때마다 균형을 맞추기 위해 트리 일부를 왼쪽 or 오른쪽으로 회전시키며 균형을 잡음
레드 블랙 트리 (Red-Black Tree)
- 자가 균형 이진 탐색 트리
- 탐색, 삽입, 삭제 모두 시간복잡도가 O(logn)
- 각 노드는 빨간색 또는 검은색의 색상을 나타내는 추가 비트를 저장하여 삽입 및 삭제 중에 트리가 균형을 유지는 데 사용
- 다음과 같은 조건을 만족
- 모든 노드는 빨간색 혹은 검은색
- 루트 노드는 검은색
- 모든 단말 노드들은 검은색
- 빨간색 노드의 자식은 검은색
- No Double Red(빨간색 노드가 연속으로 나올 수 없음)
- 모든 단말 노드에서 Black Depth는 같음
- 단말 노드에서 루트 노드까지 가는 경로에서 만나는 검은색 노드의 개수가 같음
반응형
'📚 Computer Science > Data Structure' 카테고리의 다른 글
| [자료구조] 우선순위 큐(Priority Queue) (0) | 2023.03.13 |
|---|---|
| [자료구조] 힙(Heap) (0) | 2023.03.13 |
| [자료구조] 그래프(Graph) (0) | 2023.03.08 |
| [자료구조] Time Complexity (시간 복잡도) (0) | 2023.03.07 |
| [자료구조] 큐(Queue) (0) | 2023.03.06 |