반응형
해시 테이블(Hash Table)
- 해시 테이블은 (Key, Value)식으로 데이터를 저장하는 자료구조
- 해시함수(Hash Function)를 사용하여 변환한 값을 index로 삼음
- 해시 함수(Hash Function)를 사용해 Key 값을 색인(index)으로 변환하는 과정을 해싱(Hashing)이라고 함
- 대표적인 예로 파이썬의 dictionary, 루비의 Hash, 자바의 Map 등이 있음
해시 테이블의 특징
- 기본 연산으로는 search, insert, delete가 있음
- 순차적으로 데이터를 저장하지 않음
- key를 통해서 value를 얻을 수 있음 => 이진탐색트리나 배열에 비해 속도가 빠름
- 커다란 데이터를 해시해서 짧은 길이로 축약할 수 있기 때문에 데이터를 비교할 때 효율적
- value는 중복 가능하지만 key는 유니크해야 함
- 수정 가능 (mutable)
- 삽입, 삭제 탐색 시 평균적으로 O(1)의 시간 복잡도를 가짐
해시 함수(Hash Function)
- 고유한 인덱스 값을 설정
- 임의의 길이를 갖는 메시지를 입력받아서 고정된 길이의 해시값을 출력하는 함수
- 해시 함수는 입력값의 길이가 어떻든 고정된 길이의 값을 출력하기 때문에 입력값이 다르더라도 같은 결괏값이 나오는 경우가 발생
- 해시 충돌(hash collision)이라고 표현
- 충돌이 적은 해시함수가 좋은 해시 함수
- 대표적인 해시 함수
- Division Method
- Key를 테이블의 크기로 나누어 나온 나머지를 인덱스로 사용 (index = Key % 테이블 크기)
- 테이블의 크기를 소수(Prime Number)로 정하고 2의 제곱수와 먼 값을 사용하는 것이 효과가 좋음
- ex- Key 값이 23일 때 테이블 사이즈가 7이라면 index는 2
- Digit Folding
- 각 Key의 문자열을 ASCII 코드로 바꾸고 그 값을 합한 데이터를 테이블 내의 주소로 사용하는 방법
- Multiplication Method
- 숫자로 된 Key값 K와 0과 1 사이의 실수 A, 보통 2의 제곱수인 m을 사용하여 다음과 같은 계산을 함
- index=(k*Amod1)*m
- Univeral Hashing
- 다수의 해시함수를 만들어 집합 H에 넣어두고, 무작위로 해시함수를 선택해 해시값을 만드는 기법
- Division Method
해시 충돌(Hash Collision)
- 해시 함수를 통해 index값을 구했을 때 중복이 생기는 충돌이 발생할 수 있음
- 충돌이 발생했을 때의 해결법으로 분리 연결법(Separate Chaining)과 개방 주소법(Open Addressing) 등이 있음
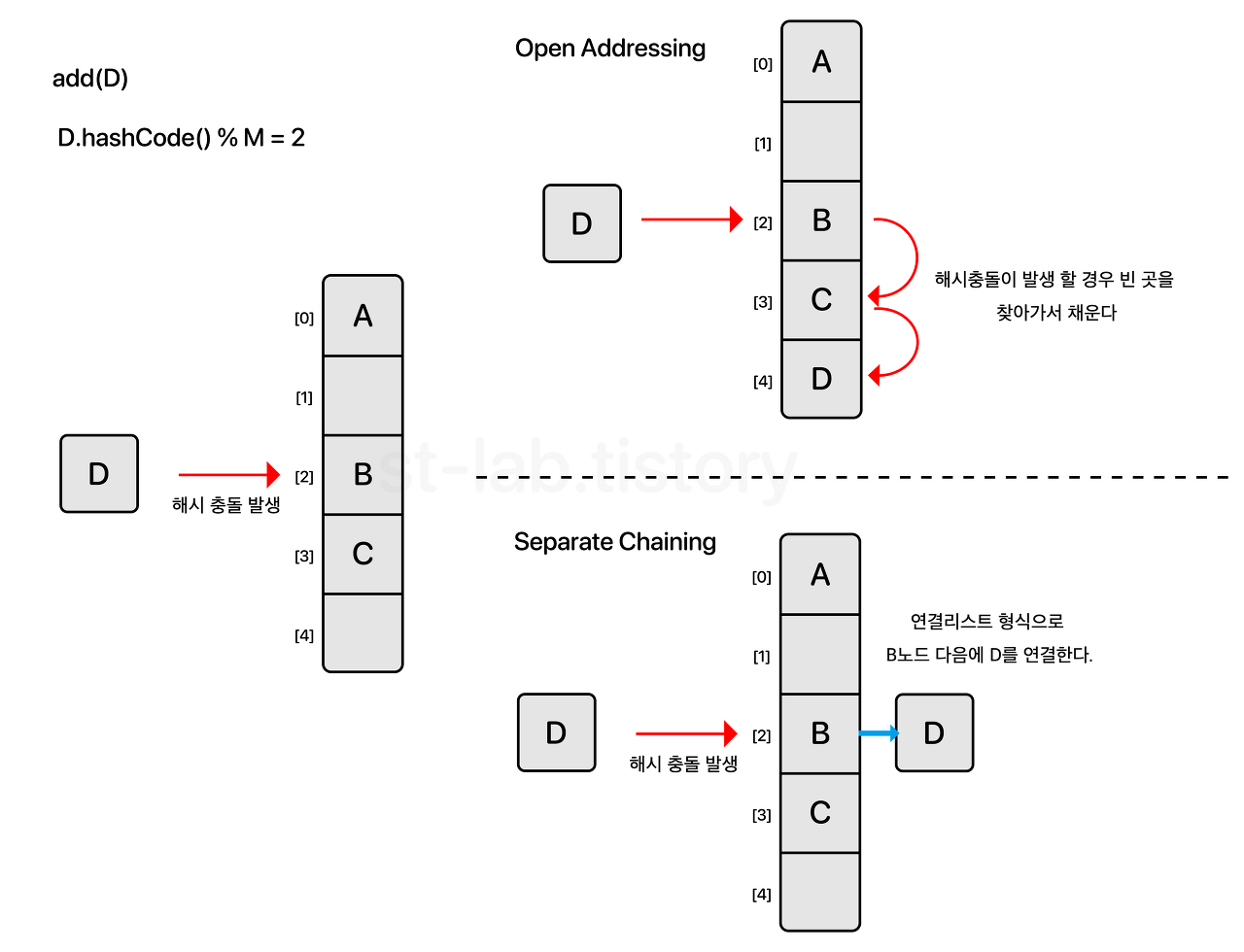
- 분리 연결법(Separate Chaining)
- 동일한 버킷(bucket)의 데이터에 대해 연결 리스트, 트리 등의 자료구조를 활용해 다음 데이터의 주소를 저장하는 것
- 한 버킷(슬롯) 당 들어갈 수 있는 엔트리의 수에 제한을 두지 않음
- 해시 충돌이 일어나더라도 linked list로 노드가 연결되기 때문에 index가 변하지 않고 데이터 개수의 제약이 없다는 장점
- 해시 테이블의 확장이 필요 없고 구현이 간단하며 원소를 쉽게 삭제할 수 있다는 장점
- 메모리 문제를 야기할 수 있으며, 테이블의 부하율에 따라 선형적으로 성능이 저하
- 부하율이 작을 경우에는 open addressing 방식이 빠름
- 개방 주소법(Open Addressing)
- 추가적인 메모리를 사용하는 chaining 방식과 다르게 비어있는 해시 테이블의 공간을 활용하는 방법
- 한 버킷 당 들어갈 수 있는 엔트리는 하나이지만 해시 함수로 얻은 주소가 아닌, 다른 주소에 데이터를 저장할 수 있도록 허용하는 방법
- 부하율(load factor)이 높을수록(= 테이블에 저장된 데이터의 밀도가 높을수록) 성능이 급격히 저하
- 개방 주소법 방식
- 선형 탐사법(Linear Probing)
- 선형으로 순차적 검색을 하는 방법
- 현재의 버킷 index로부터 고정폭만큼 이동하여 차례대로 검색해 비어 있는 버킷에 데이터를 저장
- 특정 해시 값의 주변이 모두 채워져 있는 일차 군집화(primary clustering) 문제에 취약
- 해시 충돌이 해시 값 전체에 균등하게 발생할 때 유용한 방법
- 제곱 탐사법(Quadratic Probing)
- 해시의 저장순서 폭을 제곱으로 저장하는 방식
- 예를 들어 처음 충돌이 발생한 경우 1만큼 이동하고, 그다음 충돌이 발생하면 2^2, 3^2 칸 씩 옮기는 방식
- 데이터의 밀집도가 선형 탐사법보다 낮기 때문에 다른 해시값까지 영향을 받아서 연쇄적으로 충돌이 발생할 가능성이 적음
- 선형 탐사법보다는 캐시의 성능이 떨어져서 속도의 문제가 발생
- 이중 해싱(Double Hasing Probing)
- 해시된 값을 한 번 더 해싱하여 해시의 규칙성을 없애버리는 방식(클러스터링 방지)
- 해시 함수를 이중으로 사용, 하나는 최초의 해시값을 얻을 때, 다른 하나는 해시 충돌이 일어났을 때 탐사 이동폭을 얻기 위해 사용
- 해시된 값을 한번 더 해싱하여 새로운 주소를 할당하므로 기존 방식보다 더 많은 연산을 하게 됨
- 최초 해시값이 같더라도 탐사 이동폭이 달라지고, 탐사 이동폭이 같더라도 최초 해시값이 달라져 위의 두 방법을 모두 완화 가능
- 선형 탐사법(Linear Probing)
반응형
'📚 Computer Science > Data Structure' 카테고리의 다른 글
| [자료구조] 우선순위 큐(Priority Queue) (0) | 2023.03.13 |
|---|---|
| [자료구조] 힙(Heap) (0) | 2023.03.13 |
| [자료구조] 트리(Tree) (0) | 2023.03.09 |
| [자료구조] 그래프(Graph) (0) | 2023.03.08 |
| [자료구조] Time Complexity (시간 복잡도) (0) | 2023.03.07 |